Xiufen Zou
Influence of the Binomial Crossover on Performance of Randomized Search Heuristics
Sep 29, 2021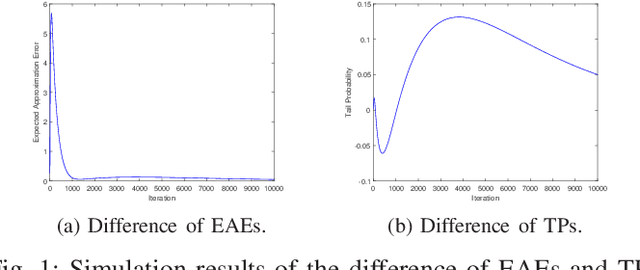
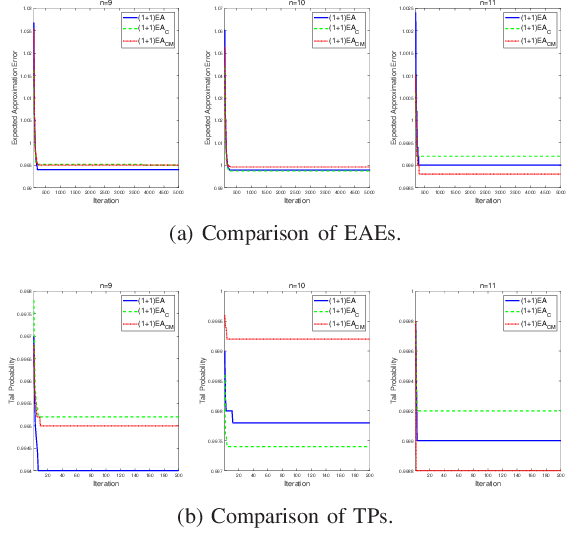
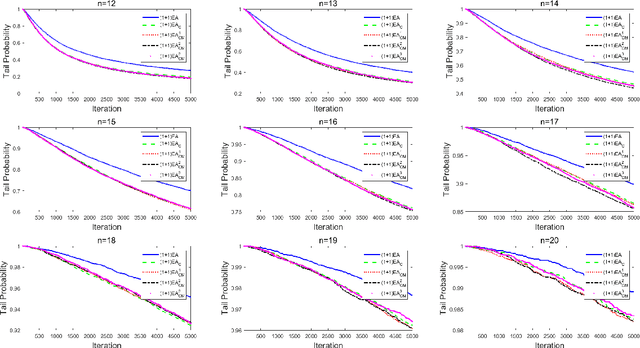
Abstract:Unlike other metaheuristics, differential Evolution (DE) employs a crossover operation filtering variables to be mutated, which contributes to its successful applications in a variety of complicated optimization problems. However, the underlying working principles of the crossover operation is not yet fully understood. In this paper, we try to reveal the influence of the binomial crossover by performing a theoretical comparison between the $(1+1)EA$ and its variants, the $(1+1)EA_{C}$ and the $(1+1)EA_{CM}$. Generally, the introduction of the binomial crossover contributes to the enhancement of the exploration ability as well as degradation of the exploitation ability, and under some conditions, leads to the dominance of the transition matrix for binary optimization problems. As a result, both the $(1+1)EA_{C}$ and the $(1+1)EA_{CM}$ outperform the $(1+1)EA$ on the unimodal OneMax problem, but do not always dominate it on the Deceptive problem. Finally, we perform exploration analysis by investigating probabilities to transfer from non-optimal statuses to the optimal status of the Deceptive problem, inspired by which adaptive strategies are proposed to improve the ability of global exploration. It suggests that incorporation of the binomial crossover could be a feasible strategy to improve the performances of randomized search heuristics.
Identification of Interaction Clusters Using a Semi-supervised Hierarchical Clustering Method
Oct 20, 2019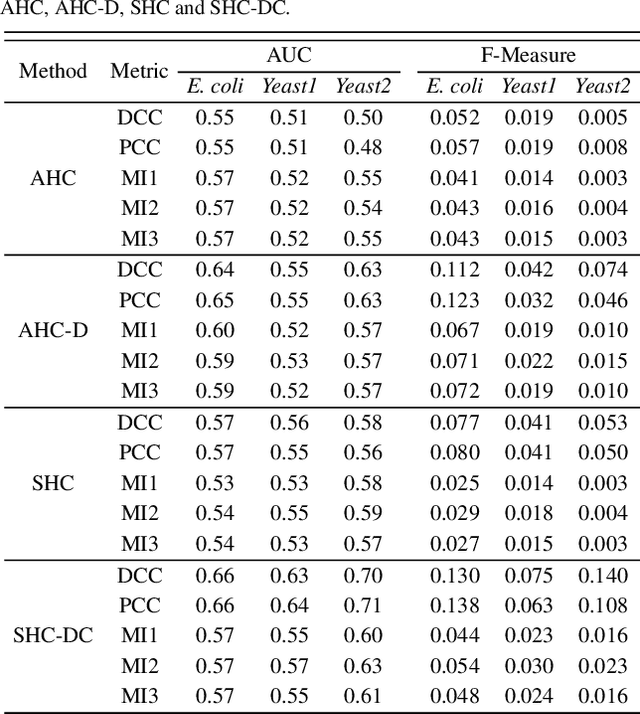
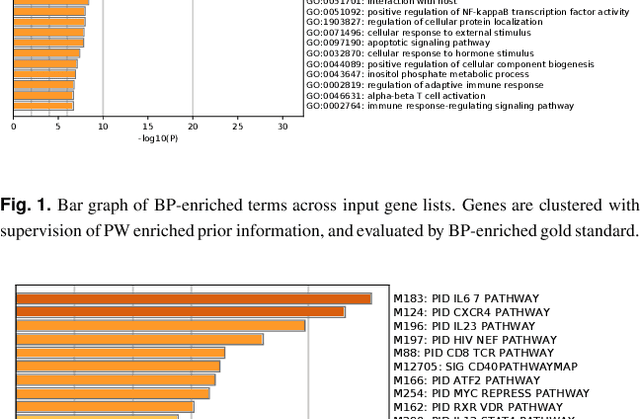
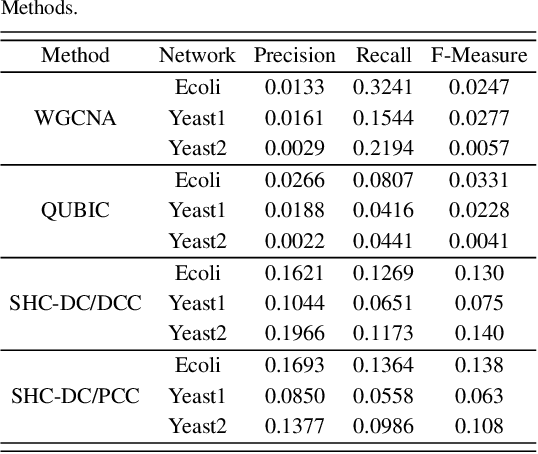
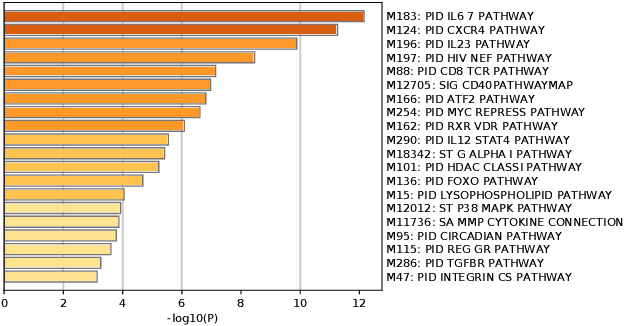
Abstract:Motivation: Identifying interaction clusters of large gene regulatory networks (GRNs) is critical for its further investigation, while this task is very challenging, attributed to data noise in experiment data, large scale of GRNs, and inconsistency between gene expression profiles and function modules, etc. It is promising to semi-supervise this process by prior information, but shortage of prior information sometimes make it very challenging. Meanwhile, it is also annoying, and sometimes impossible to discovery gold standard for evaluation of clustering results.\\ Results: With assistance of an online enrichment tool, this research proposes a semi-supervised hierarchical clustering method via deconvolved correlation matrix~(SHC-DC) to discover interaction clusters of large-scale GRNs. Three benchmark networks including a \emph{Ecoli} network and two \emph{Yeast} networks are employed to test semi-supervision scheme of the proposed method. Then, SHC-DC is utilized to cluster genes in sleep study. Results demonstrates it can find interaction modules that are generally enriched in various signal pathways. Besides the significant influence on blood level of interleukins, impact of sleep on important pathways mediated by them is also validated by the discovered interaction modules.
Inferring Gene Regulatory Network Using An Evolutionary Multi-Objective Method
Dec 16, 2015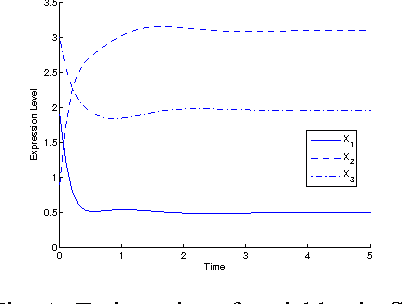
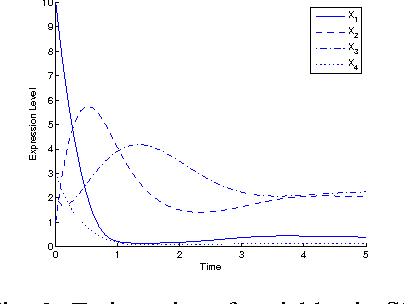
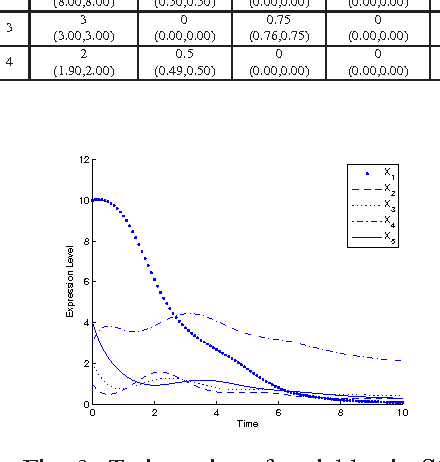
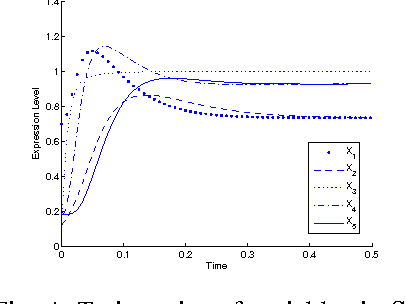
Abstract:Inference of gene regulatory networks (GRNs) based on experimental data is a challenging task in bioinformatics. In this paper, we present a bi-objective minimization model (BoMM) for inference of GRNs, where one objective is the fitting error of derivatives, and the other is the number of connections in the network. To solve the BoMM efficiently, we propose a multi-objective evolutionary algorithm (MOEA), and utilize the separable parameter estimation method (SPEM) decoupling the ordinary differential equation (ODE) system. Then, the Akaike Information Criterion (AIC) is employed to select one inference result from the obtained Pareto set. Taking the S-system as the investigated GRN model, our method can properly identify the topologies and parameter values of benchmark systems. There is no need to preset problem-dependent parameter values to obtain appropriate results, and thus, our method could be applicable to inference of various GRNs models.
A binary differential evolution algorithm learning from explored solutions
May 10, 2014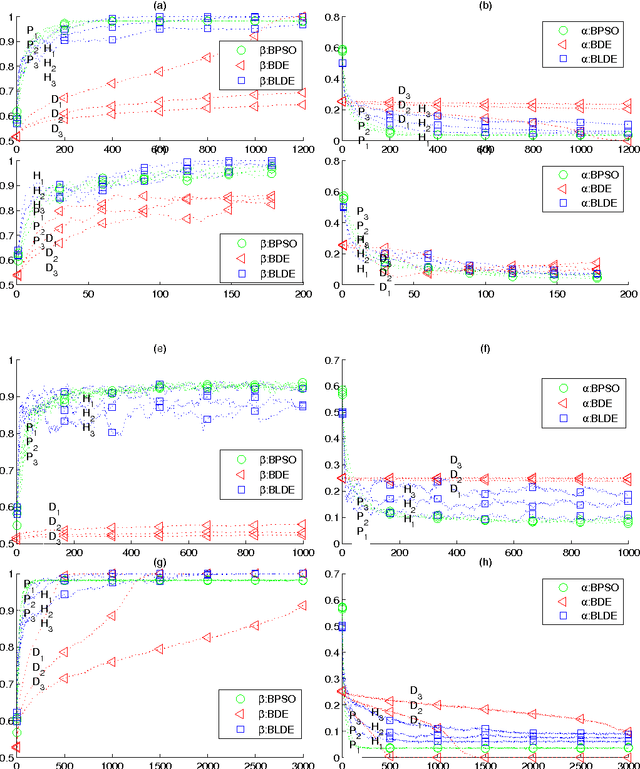
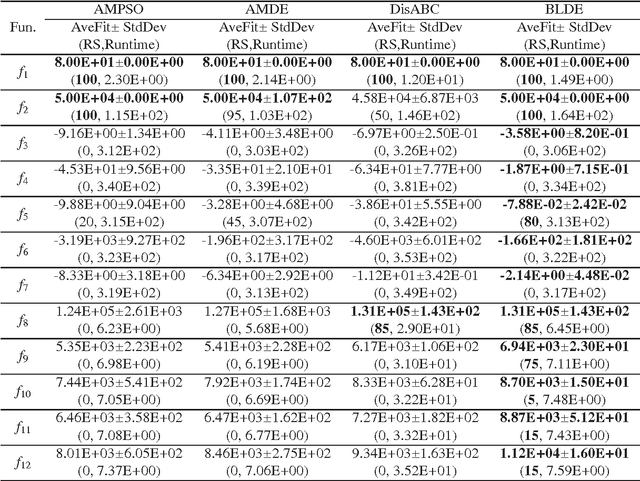
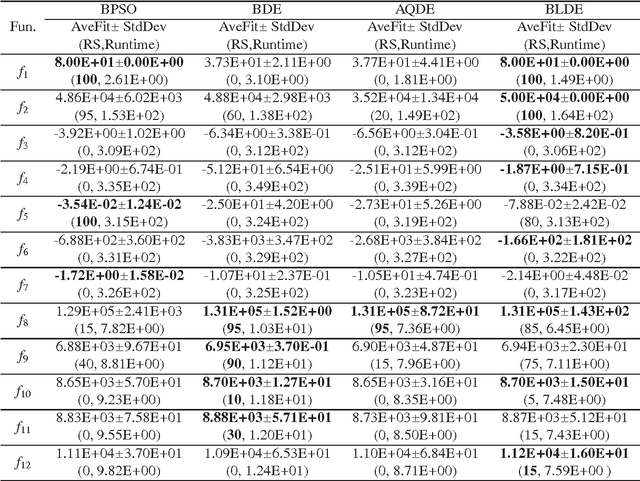

Abstract:Although real-coded differential evolution (DE) algorithms can perform well on continuous optimization problems (CoOPs), it is still a challenging task to design an efficient binary-coded DE algorithm. Inspired by the learning mechanism of particle swarm optimization (PSO) algorithms, we propose a binary learning differential evolution (BLDE) algorithm that can efficiently locate the global optimal solutions by learning from the last population. Then, we theoretically prove the global convergence of BLDE, and compare it with some existing binary-coded evolutionary algorithms (EAs) via numerical experiments. Numerical results show that BLDE is competitive to the compared EAs, and meanwhile, further study is performed via the change curves of a renewal metric and a refinement metric to investigate why BLDE cannot outperform some compared EAs for several selected benchmark problems. Finally, we employ BLDE solving the unit commitment problem (UCP) in power systems to show its applicability in practical problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge